Wuxing and Compatibility Coefficient: Part III

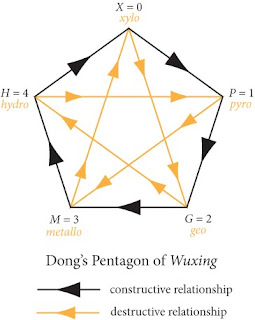
If the xing were to be arranged in a clockwise manner according to Dong's numerical order, we have the following pentagon of wuxing.


Interestingly, pentagon is the only polygon for which number of constructive relationship (number of sides) equals the number of destructive relationship (number of diagonals). This is easily proven since the only solution to the following equation:


is n = 5. Now, it is useful for a computer programmer to introduce a coefficient which can be used to compute the compatibility of any two given xing without having to refer to Dong's pentagon.

The three numerical values of compatibility coefficient cp (namely -1, 0, 1) are to be interpreted as destructive, neutral, and constructive, respectively. A convenient way to compute cp is to use the following equation:


For example, in the case of wood xing and fire xing, we have cp(0,1) = 1, a constructive relationship. In the case of fire xing and water xing, we have cp(1,4) = -1, a destructive relationship.

Comments

Post a Comment

Popular posts from this blog

「日上三竿」到底是早上多少點？

Image
從吉打 Lembah Bujang 布央谷開車回家，經過怡保的時候剛好是晚餐時間。 在麥當勞用過晚餐後，發現開車的我好像也有點睏了，於是決定在怡保睡一覺。我們把車開到 Bandar Meru Raya ，然後跟 Casuarina 要了一間房間。 隔天早我見小兒子辛円睡到很遲還不願意起床，就拿起手機給他照了一張相。 大太陽曬屁股還不起身嗎？ 原想給照片標上：阿円睡到日上三竿，大太陽曬屁股還不起身。但，住在我頭腦裡面的另外一個人問我： 三竿到底是幾點？ 於是我便上網查了一下該成語的出處：「日上三竿」應該是出自《 南齊書・天文誌上・日光色 》的一段話。《南齊書・天文誌》是南齊政府天文局官員根據每日的觀測日記整理出來的天文異象報告。《日光色》的第三個記錄是這樣寫道的： 永明五年十一月丁亥，日出高三竿， 朱色赤黃，日暈，虹抱珥直背。 這段話有三個部分。第一部分「永明五年十一月丁亥」標的是日期。第二部分「日出高三竿」說的是太陽的高度，也就是當時的時間。第三部分「朱色赤黃，日暈，虹抱珥直背」解釋的當時天文局官員觀察到的天象。 通常我讀文言文的時候都會在頭腦裡面把文字翻譯成英語。因為只有這樣，才能逼我自己將每個字都解讀出來。這段話譯成英語大概是： Sunday. December 7, 487. The shadow cast by the sun is three times the height of the pole. The colour of the sky is between red and yellow. Solar haloes and parhelia are clearly visible. 我們先說日期的那一部分。「永明」指的是南齊的 蕭宣遠 先生。蕭先生是在公元483至493期間做皇帝的。永明五年自然是落在公元487年。後面的「十一月」指的是農曆十一月，而「丁亥」是中國傳統天干地支計日系統的寫法，它是一種 60模 的寫法，例如：甲子 = 1、癸亥 = 60。所以，「丁亥」的值為24。 接著我們用 Reingold與Dershowitz 的方法把農曆日期換算成格列高曆。其結果是：公元487年12月7日（既該年的第341天，\(d = 341\)）。 根據日影我
Read more

Urusan Seri Paduka Baginda和金牌急腳遞

Image
如果你或你的公司不還稅， 內陸稅收局 的人就會寄一封公函來罵你並跟你討錢。 在馬來西亞，所有的政府公函，都會印上 Urusan Seri Paduka Baginda 的字樣。「Urusan Seri Paduka Baginda」其實是延續英國人 On His Majesty's Service 的傳統。「 Seri Paduka Baginda 」這三個字的英語是「His Majesty」或「Her Majesty」，而「Urusan」則是「Service」。 現代英國郵遞系統的原型是愛德華四世國王 Edward IV (1461-1483)設計的，他為了加快情報的傳遞速度，在大概每30km就設了一根柱子(post)和一匹新馬。這樣，情報的傳遞便能達到約2 m/s。 J. C. Hemmeon在1912年出版的《The history of the British post office》是這樣寫道的： A somewhat different style of postal service, a precursor of the modern method, was inaugurated by the fourth Edward. During the war with Scotland he found himself in need of a speedier and better system of communication between the seat of war and the seat of government. He accomplished this by placing horses at intervals of twenty miles along the great road between England and Scotland. By so doing his messengers were able to take up fresh horses along the way and his despatches were carried at the rate of a hundred miles a day. 500年前2 m
Read more

Yap-Douglas letter of 1877

Image
Water disruption at Pangkalan Lumpur In March 1877, Captain Yap Ah Loy wrote a letter to Captain W. B. Douglas (r. 1875 - 1882, Acting Resident of Selangor) to relay a water-related grievance at Pangkalan Lumpur tin mine. This letter is important because it contains several important data points: In the stamp, Captain Yap styled his residence/office as Tek Seng 德生 of Klang 吉隆. Captain Yap addressed himself with the Indic title (श्री इन्द्र प्रकाश विजय भक्ति = Sri Indra Perkasa Vijaya Bakti), and This shows that back in 150 years ago, it was perfectly reasonable for Malay courts to install their subjects with Indic titles and decorations, similar to the practices recounted in Sejarah Melayu. However, the way Yap addressed himself was not consistent, for instance, in 1881, he called himself Kaptan Cina Kuala Lumpur and not Kaptan Klang dalam Kuala Lumpur but he used his Indic title consistently. See Arkib Negara Document Number 1957/
Read more

The Sang Kancil Story of Malacca

Image
The official emblem of the state of Malacca shows two light brown mouse deers on each side of the tree of Malacca. This depiction is rather problematic. Because, if the emblem is meant to commemorate the brave Sang Kancil , as encountered by Parameswara in the Sejarah Melayu, then the color of the animal is probably not correct. If you follow the Malay classic carefully, the Sang Kancil mentioned is not light brown but white . The relatively new The logo was unveiled when Malacca was declared Historical City on April 13, 2003 logo of the City Council of Malacca, however, correctly show the two mouse deers in white . On the other hand, the Sang Kancil story purported to explain the founding of Malacca could be a story modified from a folk-tale from Sri Lanka. This fact was first noted by R. O. Winstedt (1922) Two Legends of Malacca, Journal of Straits Branch of Royal Asiatic Society, Vol. 85, p. 40. I was in the Za'ba Memorial Library , around
Read more

《心經》裡面的「般若波羅蜜」一詞

Image
很多年前曾經到過香港大嶼山的 心經簡林 。 心經簡林 是一個由三十八個巨型木簡，按數學無窮大「\(\infty\)」符號的形狀排成的木陣。在木陣裡面，除了第一個題目簡、第二十三個「空」簡和最後一個落款簡之外，其他的木簡都刻有《心經》的部分經文。 《心經》的全名叫《般若波羅蜜多心經》。我是在香港電影《 月光寶盒 》裡面，第一次聽到「般若波羅蜜多」這個詞的。在戲裡面，它是周星馳先生用來開啓可以讓時光倒流的月光寶盒的密語。必須注意的是，周先生把咒語唸成了「般若波羅蜜」，把「多」字給去掉了。 月光寶盒 的密語：般若波羅蜜. . . 不管「般若波羅蜜多」或是「般若波羅蜜」，念起來很別扭，很明顯它們都不是漢語，事實上，它們是由三個印度字組成的合成詞。「般若」的巴利語「paññā」的音譯：是知識或智慧的意思。「波羅」是巴利語「pāra」的音譯，它和英語前綴「para」一樣，是超越的意思，例如，英語「paranormal」就是超自然的意思。「蜜／蜜多」是巴利語「mī/mīta」的音譯，它是希臘語「metron」的親戚，也是英語「mete」或「measure」的祖先，想表達的是既定或肯定的意思。 把「paññā」+「pāra」+「mī」三個印度字連在一起，「般若波羅蜜」指的便是一種備受肯定、完美超凡的智慧。在周星馳先生的哲學世界裡面，也只有利用這種完美超凡的知識transcendental wisdom，才能將時空逆轉。 大嶼山的心經簡林與數學的無窮大「\(\infty\)」符號 可惜的是，我們暫時還沒有發現這種transcendental wisdom。可喜的是，數學家倒是發現了很多transcendental number（ 波羅蜜數 ）。波羅蜜數是一種很特別的數，因為你必須用無窮大「\(\infty\)」的概念才能將它正確地寫出來。例如，銀行用來算 複利息 的「\(e = 2.718\ldots\)」，就是一个波羅蜜數。 $$e = 2 + \frac{1}{1+\frac{1}{2+\frac{2}{3+\frac{3}{4+\frac{4}{5+\frac{5}{6+\frac{6}{7+\frac{7}{8+\frac{8}{9+\frac{9}{\ddots}}}}}}}}}} = 2.718\
Read more